
లెక్కలు చేస్తున్నప్పుడు గుణకారం అనేది ముఖ్యమైనది. ఇది కొంచెం కష్టంతో కూడుకున్నది. మీరు అనుకోవచ్చు గుణకారం నేను చేయగలను అని, మీరు చేయగలరు. కానీ తొందరగా చేయడానికి, నేను 30 గుణకార సూత్రాలను అందిస్తున్నాను. ఈ గుణకార సూత్రాలు సులభంగా చేయడానికి మరియు సమయాన్ని ఆదా చేయడానికి ఎంతగానో సహాయపడతాయి. ఈ లెక్కలను చేయడానికి గుణకార పట్టికను 20 వరకు నేర్చుకోవాలని నేను మీకు సిఫార్సు చేస్తున్నాను. అది సాధ్యం కాకపోతే, మీరు తప్పకుండ 9వ పట్టిక వరకు నేర్చుకోవాలి.
మీ లెక్కలను వేగవంతం చేయడానికి గుణకార గేమ్స్ ని ఆడండి . ఇప్పుడు Android అప్లికేషన్లు గుణాకర సాధన కోసం గేమ్లను అందిస్తున్నాయి. ఎలివేట్ వంటి ఆండ్రాయిడ్ యాప్లను ప్రయత్నించండి. మీరు ఎలివేట్ యాప్లో గేమ్లు ఆడితే, గుణకార సాధన కూడా జరుగుతుంది. మీరు గుర్తుంచుకోవాల్సిన గుణకార చాట్లను నేను క్రింద అందించాను.
గమనిక: కంటెంట్ సూచికను చూపించడానికి Show/Hide బటన్పై చేయండి.
Multiplication is important and difficult while doing simplifications. I have provided 30 multiplication tricks. Multiplication tricks are
1. Multiplication of Single Digit Numbers
2. Multiplication of Two-Digit Numbers
3. Multiplication of Three Digit Numbers
4. Multiplication of Four-Digit Numbers
5. Distribution Method
6. Giving and Taking Method
7. Multiplication of the Same Number
8. Multiplication of any Number between 12 and 19
9. Multiplication of 11
10. Multiplication of 111
11. Multiplication of 1111
12. Multiplication of 5
13. Multiplication of 50
14. Multiplication of 500
15. Ending with 5 and Difference 10
16. Ending with 5 and Same Number
17. Multiplication Near Value 50
18. Multiplication of the Same Number Near the Value of 100, 200, 300,400
19. Multiplication of 37 with 3 Tables
20. Common Digit Number is Greater than the Normal Number
21. Checksum Method for Verification
22. Increasing 3’s Multiplication Method
23. Increasing 6’s Multiplication Method
24. Increasing 9’s Multiplication Method
25. Sequential Inputs of Numbers with 9 (1’S)
26. Sequential Inputs of Numbers with 9 (8’S)
27. Multiplication Series of Numbers Without 8
28. Numerical Palindrome with 1’s
29. Multiply two digits numbers ending in 1
30. Common Sense Method for Multiplication
BODAMAS Rules
1. Multiplication of Single Digit Numbers:
సింగిల్ డిజిట్ నంబర్ గుణకారం గురించి వివరించాల్సిన అవసరం లేదని నాకు తెలుసు. మీ అందరికీ తెలిసిన పద్ధతి సింగిల్ డిజిట్ గుణకారం . వేగవంతమైన గణనల కోసం నేను మీకు ఒక సాధారణ ఉపాయం చెప్పాలనుకుంటున్నాను .
నేను మీకు వివరణతో ఒక ఉదాహరణ ఇవ్వాలనుకుంటున్నాను. చూద్దాము,
4×6 6×4 కంటే ఎక్కువ సమయం పడుతుంది. కాబట్టి పెద్ద సంఖ్యలతో గుణకారం చేయడానికి ప్రయత్నించండి . మీకు గుణకారం బాగా తెలిస్తే, మీరు ఏదైనా ఫార్మాట్ చేయవచ్చు. ఈ ట్రిక్ ఫాస్ట్ లెక్కలు మరియు ప్రారంభకులకు మాత్రమే.
సింగిల్-డిజిట్ గుణకారం గురించి ఏమీ వివరించాల్సిన అవసరం లేదు. అర్థం చేసుకోవడానికి నేను మూడు ఉదాహరణలు ఇచ్చాను.
E.g. 6×4=24
E.g. 7×2=14
E.g. 9×7=63
2. Multiplication of Two-Digit Numbers:
రెండు-అంకెల సంఖ్యను గుణించడం అనేది సమయాన్ని ఆదా చేయడానికి నిజంగా మంచి ట్రిక్. ఎక్కువ సమయం రెండు అంకెల గుణకారం అవసరం, కాబట్టి మీరు నేర్చుకోవాలి. మూడు మరియు నాలుగు అంకెల గుణకారానికి రెండు అంకెల గుణకారాలు ప్రాథమికంగా ఉపయోగంగా ఉంటాయి.
మనం చేసే సాధారణ పద్ధతి మూడు లైన్లు. ఇక్కడ మీరు సింగిల్ లైన్తో చేయవచ్చు . చూద్దాము,
E.g.
26×32
=26×32
∴832
Steps to Solve Two Digit Multiplication:

Step1: Multiply unit digits of two numbers, i.e.6×2=12. 1 forward carries. [2]
Step2: Multiply cross of two digits and add, i.e. 2×2+6×3=22. Then add carry to 22 (from step1, i.e. 23. 2 is a carry of 23 number (from step 2). [32]
Step3: Multiply ten digit of the numbers, i.e. 2×3=6. Then add carry from previous step i.e. 6+2=8. The final value of this multiplication is [832].
3. Multiplication of Three Digit Numbers:
రెండు అంకెల గుణకారంతో పోలిస్తే మూడు అంకెల సంఖ్యను గుణించడం కొంత అధునాతన పద్ధతి. ఇది రెండు అంకెల గుణకారం యొక్క సారూప్య పద్ధతి. ఒకే తేడా ఏమిటంటే, మేము రెండు అంకెల గుణకారంతో పోల్చితే మరో అడుగు మాత్రమే అదనంగా జోడిస్తున్నాము .
సాధారణ మూడు అంకెల గుణకారం సాధారణంగా ఎక్కువ సమయం తీసుకుంటుంది. కాబట్టి మీరు మీ గణనలను వేగవంతం చేయడానికి మూడు అంకెల పద్ధతిని గుణించడం నేర్చుకోవాలి. ఉదాహరణ మరియు చేయవలసిన దశలను చూద్దాం.
E.g.
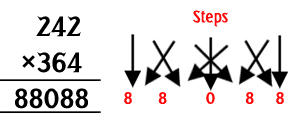
242×364
∴88088
Steps to Solve Three Digit Multiplication:
4. Multiplication of Four-Digit Numbers:
నాలుగు అంకెల సంఖ్యను గుణించడం ఒక అధునాతన పద్ధతి. ఇది అంత సులభం కాదు. ఖచ్చితమైన విలువల కోసం ఈ పద్ధతికి కొంత అభ్యాసం అవసరం. నాలుగు అంకెల గుణకారం చేయడానికి కొంచెం ఏకాగ్రత అవసరం. మీరు 7 సాధారణ దశల్లో నాలుగు అంకెల గుణకారాలను చేయవచ్చు.
కాబట్టి దయచేసి వీలైనంత ఎక్కువ సాధన చేయండి మరియు దశలను గుర్తుంచుకోండి . అభ్యాసం అవసరం, చూడటం ద్వారా మీరు కొంత సమయం వరకు ఖచ్చితమైన విలువలను పొందలేరు. మీరు అభ్యాసం లేకుండా గందరగోళానికి గురవుతారు. చూద్దాము,
E.g.
3214×1298
∴4171772
Steps to Solve Four Digit Multiplication:

5. Distribution Method:
Distribution Method ఒక అధునాతన సమయాన్ని ఆదా చేసే పద్ధతి. మీరు గుడ్డిగా వెళ్లాలనుకుంటే, మీరు రెండు-దశల గుణకారం ట్రిక్ చేయవచ్చు . ఈ ఉపాయం నేర్చుకుని సాధన చేయమని నేను మీకు సిఫార్సు చేస్తున్నాను. పంపిణీ పద్ధతి గణనలకు పెన్ మరియు కాగితం అవసరం లేదు . ఇది కరెక్ట్గా అనిపిస్తుంది. వేగవంతమైన గణనల కోసం ప్రాక్టీస్ అవసరం.
E.g.
12×17
=(12×10)+ (12×7)
=120+84
∴204
6. Giving and Taking Method:
ఇవ్వడం మరియు తీసుకోవడం కూడా అధునాతనమైనది మరియు సమయాన్ని ఆదా చేసే పద్ధతి. మీరు చాలా ఉపాయాలు నేర్చుకోవకూడదనుకుంటే, పై ఉపాయాన్ని రెండు అంకెల గుణకారం చేయండి.
నేను కొన్నిసార్లు చాలా ఉపాయాలు తగినంత అభ్యాసం లేకుండా మిమ్మల్ని గందరగోళానికి గురిచేస్తాయని అంగీకరిస్తున్నాను. మీరు సాధన చేయగలిగితే, ఈ పోస్ట్ యొక్క అన్ని ఉపాయాలు తెలుసుకోండి. అన్ని ఉపాయాలు సిఫార్సు చేయబడ్డాయి .
విలువ 10, 20, 30, 40, 50 మొదలైన వాటికి దగ్గరగా ఉన్నప్పుడు ఈ ట్రిక్ పని చేస్తుంది . అంటే యూనిట్ అంకె తప్పనిసరిగా సున్నా అయి ఉండాలి. ఇది 50 కంటే తక్కువ ఉంటే, ఆ విలువ యొక్క ప్రతికూలతను తీసుకోండి. ఇది 50 కంటే ఎక్కువ ఉంటే, ఆ విలువను సానుకూలంగా తీసుకోండి.
E.g.
12×47
=12×(50-3)
=12×50-12×3
=600-36
∴564
E.g.
56×99
=56×(100-1)
=5600-56
∴5544
7. Multiplication of the Same Number:
ఏదైనా సంఖ్య యొక్క గుణకారం 12 మరియు 19 పద్ధతి మధ్య ఉంటుంది . మీరు గుణకారం కోసం టీన్ పద్ధతిని కూడా కాల్ చేయవచ్చు (12ని చేర్చండి). ఈ గుణకార పద్ధతి 12 మరియు 19 మధ్య ఉన్న సంఖ్యలకు వర్తిస్తుంది.
మీరు 12 మరియు 19 మధ్య ఉన్న సంఖ్యలను లెక్కించినప్పుడు, ఈ ఉపాయాన్ని వర్తించండి.
It looks usual method.
E.g.
362=0936+0360
∴1296
Steps to solve Multiplication of same number
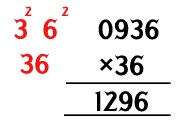
8. Multiplication of any Number between 12 and 19:
ఏదైనా సంఖ్య యొక్క గుణకారం 12 మరియు 19 పద్ధతి మధ్య ఉంటుంది . మీరు గుణకారం కోసం టీన్ పద్ధతిని కూడా కాల్ చేయవచ్చు (12ని చేర్చండి). ఈ గుణకార పద్ధతి 12 మరియు 19 మధ్య ఉన్న సంఖ్యలకు వర్తిస్తుంది.
మీరు 12 మరియు 19 మధ్య ఉన్న సంఖ్యలను లెక్కించినప్పుడు, ఈ ఉపాయాన్ని వర్తించండి.
అదే సంఖ్య యొక్క గుణకారం ఒక సంఖ్య యొక్క వర్గము. ఈ ట్రిక్ నేర్చుకోవాల్సిన అవసరం లేదు. ఇప్పుడు నేను మీకు అవగాహన కోసం మాత్రమే చెప్తున్నాను. కొన్నిసార్లు ఇది సమయాన్ని ఆదా చేసే పద్ధతి కూడా.
ప్రతి పద్ధతి మరియు ట్రిక్ నేర్చుకోండి, కానీ నేను మీకు సూచిస్తున్నాను, బాగా సాధన చేయండి. అభ్యాసం చేయకూడదనుకుంటే, సాధారణ పద్ధతులతో వెళ్ళండి . అభ్యాసం లేకుండా ఉపాయాలు ఎక్కడ ఉపయోగించాలో మీకు తెలియదు.
ఇది సాధారణ పద్ధతిగా కనిపిస్తుంది.
E.g.
14×17
Step1: Multiply unit digit of two numbers. 4×7=28 (2 carry). [8]
Step2: Add 14 and another number unit number i.e. 14+7=21. then add 21 and previous step carry i.e 21+2=23. [238]
9. Multiplication of 11:
ఏదైనా సంఖ్యతో 11 ని గుణించడం సులభం. ఇది సులభమైనది మరియు సమయాన్ని ఆదా చేసే పద్ధతి. ఇది మూడు మరియు నాలుగు అంకెల పద్ధతికి ప్రాథమికమైనది. మూడు మరియు నాలుగు అంకెల 11 గుణకారాన్ని అర్థం చేసుకోవడానికి మీరు దీన్ని నేర్చుకోవాలి.
E.g.
11×345
∴3795
Step1: First digit is take as it is 5. [5]
Step2: It is two digit 1's. So add two digits every time. Add 4+5=9.{95]
Step3: Add next two digits 3+4=7. [795]
Step4: Take last digit as it is 3. [3795]
10. Multiplication of 111:
111 గుణకారం అధునాతన పద్ధతి. ఇది 11 గుణకారం అంటే మునుపటి పద్ధతిని పోలి ఉంటుంది.
E.g.
111×873
∴96903
11. Multiplication of 1111:
1111 యొక్క గుణకారం పెద్ద సంఖ్యల కోసం అధునాతన పద్ధతి. ఇది కూడా పై రెండు పద్ధతులను పోలి ఉంటుంది.
E.g.
1111×5365
∴5960515
12. Multiplication of 5:
5 పద్ధతిని గుణించడం సులభం . ఇది పెద్ద సంఖ్యలకు ఉపయోగపడుతుంది. ఈ పద్ధతి తదుపరి స్థాయి పద్ధతులకు ప్రాథమికమైనది. పెద్ద సంఖ్యల కోసం గుణకారం ఎక్కువ సమయం పడుతుంది. ఈ పద్ధతి మీ సమయాన్ని ఆదా చేయడానికి సహాయపడుతుంది.
మీరు పెద్ద సంఖ్య అయిన ఏ సంఖ్యకైనా 2 సెకన్లలోపు సమాధానం ఇవ్వవచ్చు.
E.g.
428×5
=428/2×10
∴2140
13. Multiplication of 50:
ఇది పై పద్ధతిని పోలి ఉంటుంది. మేము యూనిట్ అంకెల సున్నాని 5కి జోడిస్తున్నాము. 50ని గుణించడం అంటే 5 కుడితో పోలిస్తే ఇది పెద్ద సంఖ్య .
E.g.
18×50
=18/2×100
∴900
14. Multiplication of 500:
ఇది పైన పేర్కొన్న రెండు పద్ధతులను పోలి ఉంటుంది. అవగాహన కోసం నేను మరో సున్నాని పెంచాను. 500 అంటే పై రెండు పద్ధతులతో పోలిస్తే ఇది పెద్ద సంఖ్య. ఈ పద్ధతి కోసం నేను పైన పేర్కొన్న రెండు పద్ధతులను వివరించాను.
15. Ending with 5 and Difference 10:
5తో ముగుస్తుంది మరియు వ్యత్యాసం 10. ఈ పద్ధతి గమ్మత్తైనది . మీరు ఈ పద్ధతిని వర్తించే ముందు తనిఖీ చేయాలి, పద్ధతి యొక్క పరిస్థితులు సంతృప్తికరంగా ఉన్నాయా లేదా.
E.g.
45×35
=(4+1)×3=15
∴1575
16. Ending with 5 and Same Number:
5 మరియు అదే సంఖ్యతో ముగియడం పై పద్ధతిని పోలి ఉంటుంది కానీ 100% కాదు. సారూప్యత ముగింపు యూనిట్ అంకెల సంఖ్య 5 . ఈ పద్ధతి కూడా కొంత గమ్మత్తైనది. ఈ పద్ధతిని వర్తించే ముందు అన్ని షరతులు సంతృప్తికరంగా ఉన్నాయో లేదో తనిఖీ చేయండి.
17. Multiplication Near Value 50:
సంఖ్య యొక్క గుణకారం అంటే 50 విలువ దగ్గర . ఇది నేను పైన చెప్పిన దానికి పూర్తిగా భిన్నమైన పద్ధతి. ఇది సాధారణ గణితం.
47 అనేది 50కి సమీపంలో ఉంది, మీరు 3 నుండి 47ని జోడించగలిగితే అది 50 అవుతుంది. కాబట్టి 47 నుండి 3ని తీసివేసి 47కి జోడించండి. అప్పుడు మీ గుణకారం 44×50 లాగా కనిపిస్తుంది. ఇప్పుడు గుణకారం సులభం.
E.g.
(47)2
=47×47
=44×50
=2200
// 32=9
∴2200+9=2209
18. Multiplication of the Same Number Near the Value of 100, 200, 300,400….
అదే సంఖ్య యొక్క గుణకారం, అంటే 100, 200, 300 మొదలైన వాటి విలువకు సమీపంలో ఉంటుంది. ఇది పైన పేర్కొన్న పద్ధతిలో సారూప్యమైనది కానీ కొంచెం సంక్లిష్టమైనది . మీరు సాధన చేయగలిగితే అది కూడా సులభం.
ఒక ఉదాహరణ చూద్దాం, నేను 86 చదరపు తీసుకుంటున్నాను. ఇది 100 విలువకు సమీపంలో ఉంది. 100తో పోలిస్తే 86 విలువ 14 తక్కువ. తర్వాత 14 విలువను మైనస్ గుర్తుగా తీసుకుని (14×14) గుణించండి. నేను మీకు సరళమైన దశలతో చెబుతాను .
E.g.
86
86 | -14
86 | -14
72 | 196 (1 is carry)
7396
19. Multiplication of 37 with 3 Tables:
3 పట్టికలతో 37ని గుణించడం అనేది ముందస్తు సమయాన్ని ఆదా చేసే పద్ధతి . దీని అర్థం 37 మరియు ఏదైనా సంఖ్యను 3తో గుణిస్తే, గుణకార పద్ధతి. ఈ పద్ధతి 3 యొక్క ఉత్పత్తిని మాత్రమే పని చేస్తుంది. ఇది చాలా సులభం.
E.g.
37×3
=7×3=21 {Multiply unit digits] ∴Take last digit i.e. 111
E.g.
37×9
=7×9=63 [Multiply unit digits]
∴Take last digit i.e. 333
E.g.
37×21
=7×21 [Multiply unit digits]
=147
∴Take last digit 777
20. Common Digit Number is Greater than the Normal Number:
సాధారణ సంఖ్య పద్ధతి కంటే సాధారణ అంకెల సంఖ్య చాలా ఎక్కువ సమయం ఆదా చేస్తుంది. ఇది ఒకే అంకెలు మరియు ఇతర సంఖ్య కంటే పెద్దది అయిన ఒక సంఖ్య మాత్రమే పని చేస్తుంది. దిగువ ఉదాహరణ సంఖ్యను చూడండి
ఇది పెద్దదిగా కనిపిస్తోంది కానీ మీరు 2 సెకన్లలోపు సమాధానం ఇవ్వగలరు.
నీకు నమ్మకం లేదా? చూద్దాము,
E.g.
5732×9999
=5732<9999
∴57314268
21. Checksum Method for Verification:
Checksum పద్ధతి అన్ని గుణకారాలకు ఉపయోగపడుతుంది. ఎలా చేయాలో మరియు ఎలా పని చేస్తుందో తెలుసుకోండి. పైన నేను పెద్ద సంఖ్యకు గుణకారం చేసాను. అది సరైనది కావచ్చు లేదా తప్పు కావచ్చు. గుణకారం యొక్క ధృవీకరణ కోసం చెక్సమ్ పద్ధతి ఉపయోగించబడుతుంది . మాకు 5732×9999=57314268 (మునుపటి పద్ధతి) వచ్చింది.
గుణకార చిహ్నాన్ని వేరు చేసే ప్రతి వైపు సంఖ్యల ప్రతి అంకెలను జోడించండి. గుణకార చిహ్నం లేకపోతే, మీరు అన్ని అంకెలను జోడించవచ్చు.
E.g.
5732×9999
=17×36
=8×9
=72
=7+2
∴9 Satisfied
22. Increasing 3’s Multiplication Method:
3 యొక్క గుణకార పద్ధతిని పెంచడం సులభం మరియు ఎటువంటి గణన చేయవలసిన అవసరం లేదు. నేను మీకు చెప్పే కొన్ని లాజిక్లతో మీరు ఈ సంఖ్యలను గుర్తుంచుకోవాలి.
మొదటి (3) విలువ యొక్క స్క్వేర్ 09. అది ఎలా పెరుగుతుందో విశ్లేషించండి.
E.g.
3=09
33=1089
333=110889
3333=11108889
23. Increasing 6’s Multiplication Method:
6 యొక్క గుణకార పద్ధతిని పెంచడం పైన పేర్కొన్న విధంగా ఉంటుంది. మీరు కొంత తర్కంతో విలువలను గుర్తుంచుకోవాలి. ఈ పద్ధతి కోసం ఎటువంటి లెక్కలు చేయవలసిన అవసరం లేదు.
E.g.
6=36
66=4356
666=443556
6666=44435556
24. Increasing 9’s Multiplication Method:
9 యొక్క గుణకార పద్ధతిని పెంచడం కూడా పై రెండు పద్ధతులను పోలి ఉంటుంది. నేను పేర్కొన్న దిగువ విలువలను గుర్తుంచుకోండి. దయచేసి పెద్ద సంఖ్యల కోసం లాజిక్ను అర్థం చేసుకోండి మరియు అనుసరించండి.
E.g.
9=81
99=9801
999=998001
9999=99980001
999999999×999999999=999999980000001
25. Sequential Inputs of Numbers with 9 (1’S):
9తో సంఖ్యల సీక్వెన్షియల్ ఇన్పుట్లు. ఇక్కడ యూనిట్లు, పదుల సంఖ్యా అంకెలను పెంచడం మరియు సంఖ్యలను జోడించడం కూడా పెరుగుతాయి. చివరగా, మీరు ఫలిత అవుట్పుట్ 1కి ఒకే విధంగా పొందుతారు. మీరు ఏ లెక్కలు అవసరం లేదని గుర్తుంచుకోవాలి .
E.g.
1×9+2=11
12×9+3=111
123×9+4=1111
1234×9+5=11111
12345×9+6=111111
123456×9+7=1111111
1234567×9+8=11111111
12345678×9+9=111111111
123456789+10=1111111111
26. Sequential Inputs of Numbers with 9 (8’S):
9తో సంఖ్యల సీక్వెన్షియల్ ఇన్పుట్లు. ఇది పై పద్ధతిని పోలి ఉంటుంది. పై పద్ధతిలో, సీక్వెన్షియల్ ఇన్పుట్లు ఆరోహణ క్రమం (1234). ఇక్కడ సీక్వెన్షియల్ ఇన్పుట్లు అవరోహణ క్రమం (987).
ఏ గణన చేయవలసిన అవసరం లేదు, మీరు గుర్తుంచుకోవాలి.
E.g.
9×9+7=88
98×9+6=888
987×9+5=8888
9876×9+4=88888
98765×9+3=888888
987654×9+2=8888888
9876543×9+1=88888888
98765432×9+0=888888888
27. Multiplication Series of Numbers Without 8:
8 లేకుండా సంఖ్యల గుణకార శ్రేణి . ఇక్కడ మనం 8 సంఖ్యల శ్రేణి లేకుండా తీసుకుంటాము మరియు 9 వ పట్టిక సంఖ్యలతో గుణించాము. చివరగా, మీరు 1లు, 2లు, 3లు, 4లు మొదలైన వాటి విలువలను పొందుతారు.
E.g.
12345679×9=111111111
12345679×18=222222222
12345679×27=333333333
12345679×36=444444444
12345679×45=555555555
12345679×54=666666666
12345679×63=777777777
12345679×72=888888888
12345679×81=999999999
28. Numerical Palindrome with 1’s:
1 యొక్క పద్ధతితో సంఖ్యా పాలిండ్రోమ్ చాలా సులభం, నేను 1 యొక్క గుణకార పద్ధతి పైన మోషన్ చేసాను. పాలిండ్రోమ్ గురించి మీకు తెలుసని ఆశిస్తున్నాను. ఇక్కడ నేను పాలిండ్రోమ్ గురించి ఏమీ వివరించడం లేదు.
విలువలను చూడండి, ఇది పాలిండ్రోమ్ లాగా కనిపిస్తుంది. ఏ గణన అవసరం లేదు కేవలం గుర్తుంచుకోండి
E.g.
1×1=1
11×11=121
111×111=12321
1111×1111=1234321
11111×11111=123454321
111111×111111=12345654321
1111111×1111111=1234567654321
11111111×11111111=123456787654321
111111111×111111111=12345678987654321
29. Multiply two digits numbers ending in 1
రెండు అంకెల సంఖ్యల గుణకారం అంటే ముగింపు యూనిట్ అంకెల సంఖ్య 1. రెండు సంఖ్యల యూనిట్ అంకె ఒకటిగా ఉండాలి. అప్పుడు మీరు ఈ పద్ధతిని దరఖాస్తు చేసుకోవచ్చు. ఈ పద్ధతి నాకు కూడా కొత్త. చూద్దాము
E.g.
51×31=1581
Step 1: Unit digit keep as it is 1. [1]
Step 2: Add the left digits 5+3=8. [81]
Step 3: Multiply the left digits i.e. 5×3=15. [1581]
30. Common Sense Method for Multiplication:
కామన్ సెన్స్ పద్ధతి ఆప్టిట్యూడ్ న్యూమరికల్ సింప్లిఫికేషన్లో గుణించడం. నేను ఈ పద్ధతికి అర్థం చేసుకోవడానికి మాత్రమే పేరు పెట్టాను. దయచేసి ఇంగితజ్ఞానాన్ని ఉపయోగించండి మరియు ఏ పద్ధతి అవసరమో ఎంచుకోండి.
అభ్యాసం లేకుండా పరిష్కరించడం కష్టమని నాకు తెలుసు . మీరు బాగా సాధన చేస్తే, ఇది చాలా సులభం. ఇది గుణకారం కోసం అంతిమ పద్ధతి . ఈ పద్ధతిని వర్తింపజేయడానికి మీరు అన్ని గుణకార పద్ధతులను తెలుసుకోవాలి.
నేను ఒక ఉదాహరణ ఇస్తాను, మీరు ఎలా పరిష్కరించగలరో ఆలోచించండి? ఈ ఉదాహరణను పరిష్కరించడానికి మీరు ఒకటి కంటే ఎక్కువ పద్ధతులను వర్తింపజేయాలి. చూద్దాము,
మీరు ఏవైనా లోపాలను కనుగొంటే , దయచేసి వ్యాఖ్యానించండి. దయచేసి ఈ కథనాన్ని ఇతరుల కోసం షేర్ చేయండి. Facebook పేజీ వంటి మరిన్ని అప్డేట్ల కోసం.
E.g.
33×333×3333
3×11×333×3333
11×333×9999
3663×9999
36626337
If you found any errors, Please comment. Please share this article for others. For more updates like face-book page.
 RajashekarKankanala
RajashekarKankanala.png)



 Welcome to Tuts Raja!
Welcome to Tuts Raja!



